What is Unbalance?
According to the International Organization for Standardization (ISO) unbalance or imbalance is defined as “that condition which exists in a rotor when a vibratory force or motion is imparted to its bearings as a result of centrifugal force.”
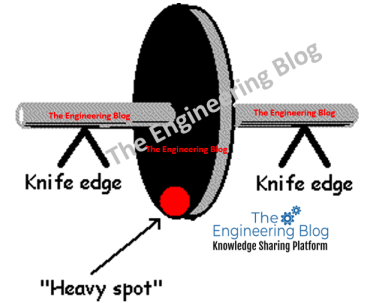
The effect occurs when a rotor’s mass is unevenly distributed about the axis of rotation. This can be envisaged as a “heavy spot” on the rotor.
Imaging the rotor of an electric motor, turbine blade, fan, crankshaft of an engine, drive shaft of a machine, or even the wheel of an automobile, all the parts are susceptible to unbalanced conditions. What will happen if an unbalanced amount goes beyond the limit? Vibrations? Additional load on the machine’s foundation or support? Failure of the machine? what if the frequency of vibrations matches the resonance frequency? we will discuss all the situations or reasons in this article.

The units of unbalance are the product of the weight of the heavy spot and the diameter at which it acts. Typically, this is expressed as either gram-millimetres or ounce-inches of unbalance. The centrifugal force generated by an unbalanced rotor is a function of the amount of unbalance and the rotor operating speed. It may be calculated by the following formulas:
For metric units:
F=0.01 x W x R x (RPM/1000)2
F = Centrifugal force in Kg
W= Unbalance weight in Kg
R= Unbalance radius (centimeters)
RPM = Rotor operating speed
For English units:
F=1.77 x W x R x (RPM/1000)2
F = Centrifugal force in pounds
W= Unbalance weight in ounces
R= Unbalance radius (inches)
RPM = Rotor operating speed
Why Unbalance is Detrimental to Rotating Machines?
Note from the above formula that the force generated varies with the square of the rotor speed. This means that doubling the speed of the rotor results in four times the force. Given the higher operating speeds of modern machinery, relatively small amounts of unbalance can result in very destructive centrifugal forces.
Now Imagine any rotor supported by bearings at the ends and having unbalanced mass. What will happen?
- With every rotation, there will be an unbalanced force getting transferred to the bearings
- This unbalanced force will damage the lubrication film inside the bearing which will result in metal-to-metal contact and ultimately early failure of bearings and machine breakdown!
- Not only this, the unbalanced force will also get transmitted to the foundation or support of the machine, causing vibrations and may even affect the nearby machines
If a rotor is placed on knife edges and allowed to rotate freely, gravity causes the rotor to come to rest with a heavy spot at the bottom. A very crude balance is achieved by simply adding weight at the location radially opposite this position until the rotor remains stationary in any position where it is placed.
Types of Unbalance
Some rotors behave like the simple disc rotor as in the below picture; however, in many cases, allowance must be made for variation in mass distribution along a rotor’s length. The unbalanced weight shifts the rotor’s principal axis of inertia parallel to the rotational axis. (The principle axis of inertia may be thought of as the axis about which the rotor’s mass is evenly distributed). This type of unbalance is referred to as static or force unbalance.

This rotor effectively has two equal and opposite unbalanced masses. When placed on knife edges, the rotor does not attempt to turn and thus appears balanced. However, in service, it imparts centrifugal forces to support bearings. In this situation, the rotor’s principal axis of inertia intersects the rotational axis at the rotor’s center of gravity. This type of unbalance is known as couple unbalance.

Similarly, there can be a situation where the rotor also has heavy spots that are radially opposite to each other, but of unequal weight. In this situation, the principal axis of inertia intersects the rotational axis at a point other than the center of gravity. This form of unbalance is known as quasi-static unbalance. It is effectively a particular combination of static and couple unbalanced.

A more common combination of static and couple unbalance is known as dynamic unbalance. Dynamic unbalance exists when the principle axis of inertia is displaced from the rotational axis so the axes are neither parallel nor do they intersect.

Causes of Unbalance
Unbalance in a rotor occurs for a variety of reasons. An understanding of how unbalance may develop is useful when undertaking balancing operations or when performing root cause failure analysis.
Deposit Build Up
Unbalance often results from a build-up of dirt or dust on fan blades. A rotor’s balance condition may change gradually, as it generally takes time for build-up to accumulate. However, the onset of unbalance may appear quite sudden. In many situations the deposit build-up may be uniform, resulting in little change to the rotor’s state of balance. Eventually, the build-up becomes so thick and heavy that pieces break away, resulting in a sudden change in balance condition.
Often, this unbalanced situation may be corrected by simply cleaning the rotor. Machine manufacturers usually facilitate this activity through the provision of an access panel or similar mechanism, which makes it possible for the rotor to be cleaned without major disassembly. Generally, rotors are cleaned during preventive maintenance of machines.
Erosion of Rotor
Rotor erosion is most commonly observed in fans or pumps that handle corrosive gases or fluids. It is likely that correction of unbalance resulting from rotor erosion is be accompanied by additional repair activity.
Turbulent flow associated with a damaged rotor may be a source of additional vibration. Therefore, it should be realized that balancing the rotor may not be enough to restore the machine to an acceptable level of vibration.
Rotor Distortion
Rotor distortion can occur for a variety of reasons. Common causes are thermal effects and unrelieved stresses induced in rotor construction during manufacture (by welding, bending, or other processes).
Including unbalance, rotor distortion may give rise to other problems (i.e. turbulent flow) so that dynamic balancing may not provide a complete solution to the problem.
Eccentricity
Eccentricity is a common source of unbalance and can arise for a variety of reasons.
Incorrect machining of a rotating part may result in a component that has an off-center borehole. Eccentricity may also arise as a result of the accumulation of manufacturing tolerances.
The below diagram shows a pulley or gear mounted on a motor shaft. Insertion of the key takes up the clearance tolerance between the bore and the shaft, which causes the weight of the pulley/gear to shift off-center.
Eccentric pulleys and gears may also cause other vibration problems. For example, an eccentric pulley causes reaction forces to be generated as the drive belt alternately tightens and then loosens. Balancing the pulley simply makes allowances for eccentricities in terms of unbalanced vibration. The reactive forces from the belt, and any vibration generated by those forces, are unaffected.

Keys and Keyways
Keys and keyways can be a source of unbalance. If the shaft and rotor (to be mounted on the shaft) are balanced without a key, then the introduction of the key on assembly results in an unbalance. It is increasingly common for rotors to be half-key balanced. (ISO standard 8821 has relevance here.)
Casting Defects
Invisible flaws in cast rotors may be a source of unbalance. Blowholes or the inclusion of sand or other foreign matter in the casting lead to uneven mass distribution and may be severe enough to require that the component be balanced.
Summary
It is inevitable that all rotors exhibit some degree of unbalance. Even if technology allowed a rotor to be perfectly balanced it would probably be cost prohibitive. The key issue is that a rotor is fit for purpose. ISO standard 1940-1 (1986) outlines balance quality requirements and the permissible level of residual unbalance for various types of rigid rotors.
Field Balancing (Step by Step)
The following discussion assumes use of a rigid rotor (a rotor that operates below 70% of its critical speed). A flexible rotor (a rotor that operates at 70% or above its critical speed) requires multiple plane balancing, which is outside the scope of this text.
In certain circumstances it is possible to balance a rotor in place using vibration measurement instruments. Many modern vibration monitoring and analysis instruments include on-board software to collect the required data, perform necessary calculations, and provide the required weight corrections. These instruments can usually be relied upon for good results; however, inaccuracies do occur. It is useful in those circumstances to have an understanding of balancing from first principles so appropriate allowance can be made for any particular influences that may be present.
Most rotors that require balancing have been balanced during manufacturing and possibly following an overhaul. Nevertheless, field balancing can enhance the balance condition of a machine. Rotors balanced in the field are balanced in their own bearings, with all parts assembled. Therefore, any unbalance caused by the accumulation of manufacturing tolerances is accounted for. Often, the workshop machine does not allow the rotor to run at its service speed, and the workshop’s support structure has a different stiffness to the rotors in service mounting. Field balancing makes allowance for influences such as thermal effects, rotor distortion under load, environmental effects, etc., and avoids the expense and time loss associated with machine disassembly.
Step 1: Preparations
Good preparation is the key to successful field balancing. A thorough inspection of the machine should be undertaken to ensure that all bolts are tight and that there are no obvious cracks or other damage. The outside and the inside of the rotor should be checked for deposit build up. Any build-up identified should be cleaned before an attempt is made to balance the rotor. Safety is paramount in balancing. Very often the field balancing process requires the machine to be operated in a disassembled state to allow access to the rotor. All care must be taken to eliminate unnecessary risks.
The rotor should be checked to identify a safe and secure method for making the necessary weight adjustments. Loose weights constitute a major safety hazard during the balancing process, and can also be highly destructive if they break away after a machine is returned to service. It is a sobering thought to realize that a four-foot diameter fan operating at one thousand RPM has a blade tip speed approaching 150 mph!
If correction is to be achieved by adding weights to the rotor then suitable trial weights should be prepared in advance, and a speedy method of supplying the final weights should be established. Field balancing requires the machine to be stopped and started several times. For this reason, field balancing can rarely be undertaken with the machine in normal production. Much time in a balancing exercise is effectively waiting time: 1). Waiting for the machine to reach operating speed 2). Waiting (perhaps) for the machine to achieve operating temperature 3). Waiting to hit the start button as the number of permissible starts per hour is limited.
Lack of adequate preparation can add greatly to waiting time if the required materials and equipment are not immediately on hand. If balancing requires adjusting rotor weight by removing material (typically drilling or grinding) then warranty issues surrounding the machine must be investigated. Drawings should be studied to ensure rotor integrity and safety is not compromised by the proposed action.
Complete a thorough vibration analysis before attempting to balance a rotor to confirm that: 1). Unbalance is indeed the problem 2). There are no additional vibrations from other issues such as flow turbulence or belt reactions that need to be corrected.
Step 2: Recognizing the Type of Unbalance
It may be possible to identify the type of unbalance from the nature of the vibration data taken from the rotor’s support bearings. The comments that follow assume a symmetrical rotor mounted symmetrically between bearings. Any asymmetry in the structure should be allowed for when considering the data.
- If the rotor were suffering from a condition of static unbalance then logically the vibration exhibits the same amplitude and phase at each support bearings.
- If the rotor is suffering from a condition of couple unbalance then the vibration amplitude at the two support bearings is the same in terms of amplitude with a phase difference of 180 degrees.
- A rotor having a quasi-static unbalance problem shows different vibration amplitudes with an accompanying phase difference of 180 degrees.
- A rotor with a dynamic unbalance exhibits no discernable relationship between the vibration amplitude and phase readings at the support bearings
Step 3: Preparing for Field Balancing Requirements
In-place rotor balancing requires the following:
- The ability to stop and start the rotor to carry out necessary calibration runs.
- Access to the rotor to add and remove weight at the required location.
- A safe and secure method of attaching required weights.
Field balancing is based on two simple assumptions that hold true for most machines:
- The machine exhibits a linear vibratory response to unbalance. In other words, the vibration generated by unbalance is directly proportional to the amount of unbalance that is present.
- The phase of the unbalanced vibration shifts through an angle equal to a shift in the angular position of the heavy spot.
Vibration instruments used for balancing should have the ability to tune in to the unbalanced component of vibration and measure its phase. There does exist a vector solution for single plane balancing that does not require phase measurements (known as the three-circle method); however, most modern vibration analyzers have phase capability so it is not widely used. This discussion assumes that phase measurements are available.
Field balancing is performed by first observing the vibration characteristics of the unbalanced rotor. The machine is then stopped and arbitrary trial weights are added. The effect of the trial weight(s) upon vibration data is then observed. This data is used to calculate the actual correction (location and amount) required.
It is customary for vibration balance calculations to be based on measurements of vibration displacement (units are mils or microns). In reality, there is no reason why field balancing calculations are not based on vibration velocity measurements provided consistency is maintained throughout the balancing operation. For the purposes of this discussion, we will conform to the convention and employ displacement measurements.
Types of Balancing (considering the number of planes)
- Single Plane Balancing (we will discuss in detail)
- Two Plane Balancing (we will discuss only the introduction)
- Multiple Plane Balancing (we will not discuss this)
Single Plane Balancing
The simple disc rotor illustrated in below Figure could be crudely balanced on knife edges as discussed earlier. It is also possible to balance the rotor in a similar fashion by observing its behavior when mounted in place, provided that it is able to rotate freely on its own bearings. A better level of balance is certainly achieved by employing calculations based on vibration measurements.
The rotor is run in its original condition, and the amplitude and phase of vibration are recorded from one of the support bearings. For the purposes of this example, we shall assume that the amplitude is 300 microns with a phase of 300 degrees. This vibration can be represented on the diagram in Figure 7 as the vector O (the length of the line is scaled to represent the amplitude, and it’s angular position to represent the phase).

An arbitrary trial weight is added to the rotor. In reality, of course, we need to ensure that the trial weight used is not too heavy to cause damage, yet heavy enough to have a measurable effect. For optimum results the trial weight should produce approximately a thirty percent change in vibration amplitude, and/or a thirty-degree change in the phase angle. Most modern balancing software includes a utility for estimating trial weight size. The calculation employed is based on rotor weight and speed, and the software is designed to ensure the centrifugal force generated by the trial weight does not exceed ten percent of the static load on the support bearings.
When the trial weight is added to the rotor one of three things could happen:
Possibility 1: Purely by chance the trial weight may be placed on the heavy spot, making it heavier. This results in a vibration amplitude increase but does not change the phase.
Possibility 2: Purely by chance the trail weight may be placed immediately opposite the heavy spot. If the trial weight is heavier than the heavy spot the vibration phase changes by 180 degrees, and some new amplitude of vibration results. If the trial weight is lighter than the heavy spot the phase does not change but the amplitude is reduced.
Possibility 3: The most likely occurrence is that the trial weight is positioned somewhere between these two positions and the resulting vibration displays a new amplitude and the phase reading is unrelated to the original data.
For the purposes of this example, assume the new readings give an amplitude of 250 microns displaying a phase of 210 degrees. This vibration results from the cumulative effect of the original rotor unbalance, plus the effect of the trial weight. This data can be plotted on the diagram in Figure 7 as the vector O+T. Joining the ends of the two vectors O and O+T gives the vector T, which represents the effect of the trial weight used.
In practice, we look for a correction weight that is equal in magnitude but opposite to the original unbalance O. Scaling the value of vector T from the diagram and using this value in the formula below, enables the correct weight to be calculated.
Correct Weight = Trial Weight x (O/T)
In this example, the value of vector T is 390 microns. Thus, the required balance weight is the trial weight x (300/390), or 0.77 times the trial weight.
The trial weight readout is in terms of multiples of the trial weight. For this reason, it does not usually matter what units of weight are used. If weighing scales are not available to support the balancing operation then it makes little difference to the balancing instrument. For example, if a washer is used as a trial weight, a trial weight value of one unit is entered into the balancing program. The balancing system’s ultimate readout of the required correction of 0.77 (weight units irrelevant) simply means the required correction is 0.77 washers.
The included angle b between vectors O and T is measured from the diagram. This represents the location of the required correction relative to the location of the trial weight. For this example, the included angle β is 40 degrees. Therefore, the result of our balancing exercise instructs us to replace the trial weight with a weight 0.77 times as heavy, and position it 40 degrees away from the location of the trial weight. The direction of movement for the correct weight location (with shaft rotation or against shaft rotation) depends upon the method employed for measuring the vibration phase. Modern software balancing systems usually present this information clearly.
The vector calculation outlined above provides the basis for today’s software-driven field balancing systems. Instruments store the data from original and trial weight runs and automatically compute the required correction.
Two-Plane Balancing
The single-plane solution outlined above holds well for narrow rotors operating at less than approximately 1000 RPM. Balancing needs to be carried out using more than one correction plane for wider rotors operating at higher speeds. Some guidelines are offered:
- If the rotor operates above 70% of its first critical speed, it should be treated as a flexible rotor that requires multiple-plane balancing (outside the scope of this document).
- A rotor requires two-plane balancing if its ratio of length to diameter is greater than 0.5 and it operate above 150 RPM.
- Long rotors (i.e. paper machine rolls) with a length/diameter ratio greater than 2 and a service speed above 100 RPM, require two plane balancing
–end of topic–
keywords: Balancing, Importance of Balancing, Single Plane Balancing, Two Plane Balancing, Multi-plane Balancing, Methods of Balancing, Field Balancing, Balancing Software, Causes of Unbalance, Types of Unbalance, Detrimental Effects of Unbalance on the Rotating Machines